Why Exponential Decay Breaks Our Brains

And What Folding a Piece of Paper Teaches Us About Eddy Current Depth of Penetration

Eddy Current Testing (ECT) has a reputation.

Among people who don’t work with it regularly, it’s often described as black magic. Not because the physics is unknowable—but because the behavior doesn’t match human intuition.

One of the biggest offenders is depth of penetration.

Most people understand the formula.
Far fewer truly understand the behavior.

That gap—between knowing the equation and grasping what it actually means—is where bad inspection assumptions are born.

Eddy Currents Don’t Fade Linearly

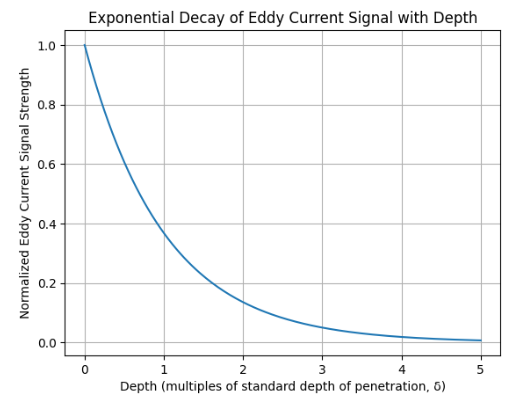
Figure 1 — Exponential decay of eddy current signal strength with depth
The signal does not decrease at a constant rate. Each additional standard depth of penetration (δ) reduces the remaining signal by a fixed percentage, causing rapid collapse after only a few depths.

• At 1δ, the signal is already down to about 37%

• At 2δ, only ~14% remains

• At 3δ, you’re below 5%

• Beyond this point, signal-to-noise—not physics—becomes the limiting factor.

In eddy current testing, induced currents are strongest at the surface of a conductive material and weaken as they penetrate deeper into it.

But here’s the critical detail:

     Eddy current strength does not decrease linearly with depth.
     It decreases exponentially.

At one standard depth of penetration (δ), the current density has already dropped to about 37% of its surface value.
At two depths, it’s about 14%.
At three depths, roughly 5%.

After just a few depths, the signal hasn’t merely weakened—it has collapsed.

This is why statements like:

“   We should still see something at that depth.”

often sound reasonable… but are physically wrong.

The Problem Isn’t the Math — It’s Us

Humans evolved to understand linear cause and effect:

• Double the effort → double the result

• Go twice as far → burn twice the energy

Exponential behavior doesn’t feel natural to us, which is why it repeatedly surprises people in areas like:

• Radioactive decay

• Heat transfer

• Signal attenuation

• Finance

• Population growth

And yes—eddy current testing.

To really understand exponential behavior, it helps to step away from NDT for a moment.

Compound Interest: Exponential Growth Everyone Talks About (But Few Feel)

Most people know compound interest is powerful.

But early on, it looks boring.

Money grows slowly at first because the growth is based on a percentage of a small amount. Later, that same percentage is applied to a much larger base—and things accelerate rapidly.

That curve doesn’t rise steadily.
It takes off.

Now let’s flip that idea on its head.

Eddy Current Attenuation Is Compound Interest in Reverse

Depth of penetration behaves like negative compound interest.

Each additional increment of depth doesn’t reduce signal strength by a fixed amount. It reduces it by a percentage of what remains.

That means small changes in depth can produce dramatic changes in signal response.

To see just how unintuitive this is, let’s look at a thought experiment that famously breaks brains.

The Paper Folding Experiment (This Is Where Things Get Weird)

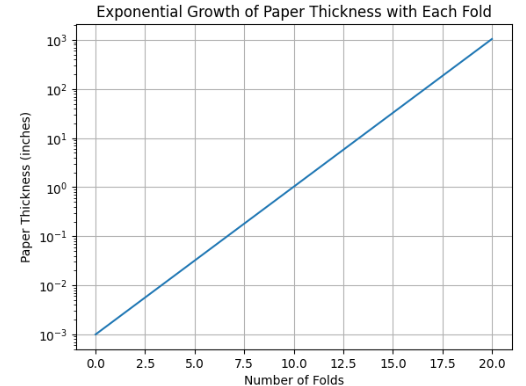
Start with a single sheet of paper.

Assume it’s 0.001 inches thick.

Each time you fold it in half, the thickness doubles.

The First Few Folds (Nothing Alarming)

• 0 folds → 0.001 inches

• 1 fold    → 0.002 inches

• 2 folds → 0.004 inches

• 3 folds → 0.008 inches

• 4 folds → 0.016 inches

• 5 folds → 0.032 inches

• 6 folds → 0.064 inches

• 7 folds → 0.128 inches

• 8 folds → 0.256 inches

• 9 folds → 0.512 inches

• 10 folds → 1.024 inches

After 10 folds, your paper is just over 1 inch thick.

So far, nothing seems outrageous.
That’s exactly the trap.

Exponential Growth Quietly Turns Violent

Let’s keep folding.

• 15 folds → 32.8 inches (~2.7 feet)

• 20 folds → 1,048 inches (~87 feet)

• 25 folds → 33,554 inches (~0.53 miles)

• 30 folds → 1,073,742 inches (~16.9 miles)

Just 30 folds would give you a stack of paper taller than Mount Everest.

And we’re nowhere near done.

Now We Leave the Planet

• 40 folds → ~17,000 miles
  (more than halfway around the Earth)

• 42 folds → ~44,000 miles
  (around the entire Earth)

• 45 folds → ~350,000 miles
  (almost to the Moon)

• 50 folds → ~22 million miles
  (a significant fraction of the distance to the Sun)

And remember—we started with a sheet of paper.

What Happens at 100 Folds?

Mathematically:

Thickness =
0.001 × 2¹⁰⁰ inches

2¹⁰⁰ ≈ 1.27 × 10³⁰

That yields a thickness of roughly:

    1.27 × 10²⁷ inches

Converted to miles:

    ~2 × 10²² miles

For perspective:

• Earth to Sun ≈ 93 million miles

• One light-year ≈ 5.88 trillion miles

• Diameter of the Milky Way ≈ 100,000 light-years

At 100 folds, your paper would extend millions of times farther than the Milky Way galaxy.

That’s not exaggeration.
That’s exponential math.